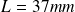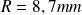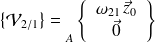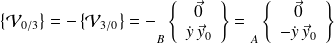Exploitation du schéma cinématique : la loi entrée/sortie
Définition
Fondamental : loi entrée/sortie
Une loi entrée-sortie géométrique est une relation entre les paramètres de position et/ou d'orientation de la classe d'équivalence recevant le mouvement d'entrée et ceux de la classe d'équivalence communiquant le mouvement de sortie.
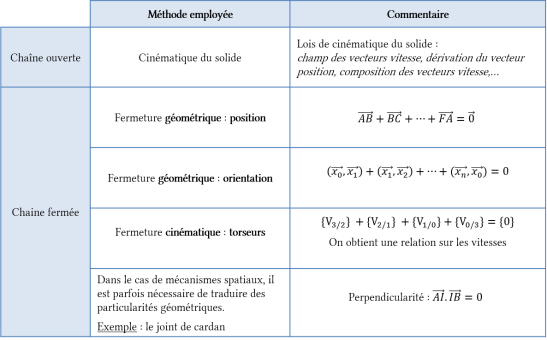
Selon le type de chaîne cinématique de solides rencontré, différentes méthodes peuvent être employées :
Exemple d'une chaîne cinématique ouverte : bras robot

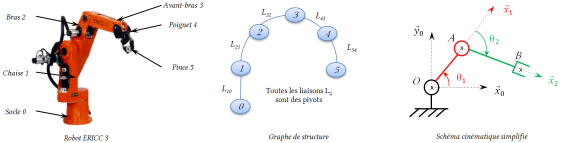
On considère le modèle plan simplifié dans lequel la pince de robot n'est animée que par deux mouvements de rotation paramétrés par
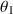 et
et
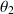 .
.
Chaque bras du robot est de longueur
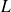 . On utilise le système de coordonnées cartésiennes pour positionner le point
. On utilise le système de coordonnées cartésiennes pour positionner le point
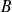 en bout de chaîne dans le repère
en bout de chaîne dans le repère
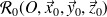 . Ainsi
. Ainsi


→ Relation directe : le modèle géométrique direct permet d'exprimer les paramètres de sortie
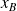 et
et
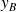 en fonction des paramètres d'entrée
en fonction des paramètres d'entrée
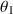 et
et
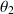 .
.

D'après la relation de Chasles :
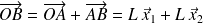 .
.
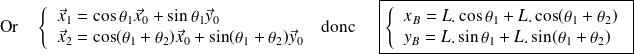

→ Relation indirecte : le modèle géométrique indirect permet d'exprimer les paramètres d'entrée
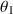 et
et
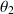 en fonction des paramètres de sortie
en fonction des paramètres de sortie
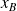 et
et
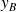 .
.

On part de la relation directe :
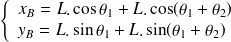
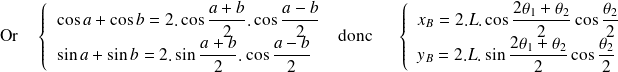

La suite du calcul se déroule en deux étapes :
Dans un premier temps on calcul
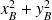 pour faire apparaître des termes du type
pour faire apparaître des termes du type
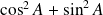 et obtenir une expression indépendante de
et obtenir une expression indépendante de
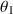 :
: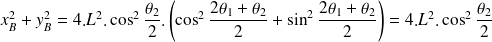
Et comme
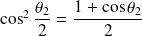 , on trouve
, on trouve
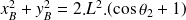
Soit
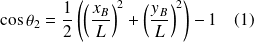

Dans un second temps, on calcul le rapport entre les composantes
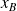 et
et
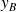 :
: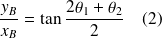
Conclusion : de
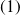 et
et
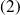 , on déduit :
, on déduit :
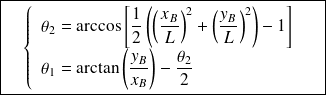
Exemple d'une chaîne cinématique fermée : micromoteur de modélisme
Hypothèse simplificatrice : problème plan
On suppose pour cette étude que le problème est plan, dans le plan :
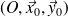 .
.
On admettra que dans ces conditions, la liaison pivot glissant d'axe
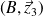 entre le piston
entre le piston
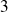 et la bielle
et la bielle
 soit simplifiée en une liaison pivot glissant d'axe
soit simplifiée en une liaison pivot glissant d'axe
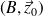 .
.
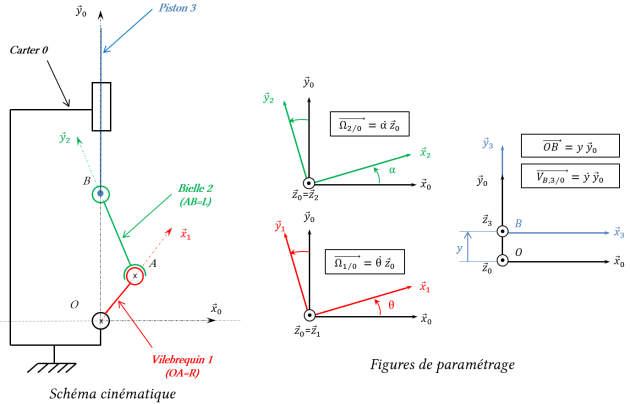
L'hypothèse du problème plan permet de simplifier les torseurs cinématiques des liaisons suivantes :
Liaison sphérique de centre A entre la bielle
 et le vilebrequin
et le vilebrequin
 :
: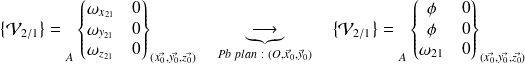
Liaison pivot glissant d'axe
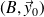 entre le piston
entre le piston
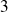 et le carter
et le carter
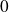 :
: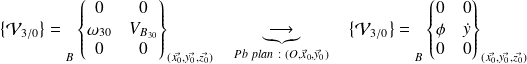
Liaison pivot glissant d'axe
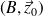 entre le piston
entre le piston
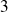 et la bielle
et la bielle
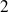 :
: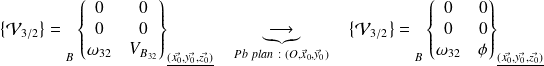
Fermeture géométrique
paramètre d'entrée : position linéaire
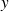 du piston
du piston
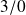
paramètre de sortie : position angulaire
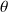 du vilebrequin
du vilebrequin
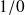
Relation de fermeture géométrique :
On projette cette expression :
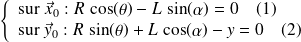
Pour obtenir la loi entrée sortie, il faut relier les paramètres d'entrée et de sortie en éliminant le paramètre
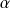 . Une méthode efficace consiste à utiliser le fait que
. Une méthode efficace consiste à utiliser le fait que
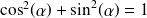 :
:
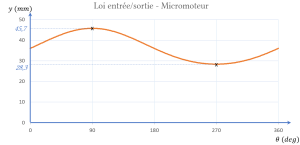
d'où la loi entrée/sortie géométrique :
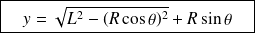 , valable pour
, valable pour
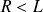 .
.
Fermeture cinématique
Traduction de la fermeture cinématique de la chaîne :
Pour pouvoir additionner des torseurs, ceux-ci doivent être réduits au même point, par exemple au point A.
En tenant compte de l'hypothèse du problème plan dans le plan
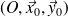 , on obtient :
, on obtient :
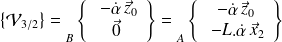
car
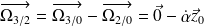
et
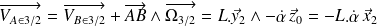
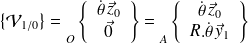
car
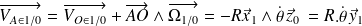
Ainsi la fermeture cinématique nous donne deux équations vectorielles :
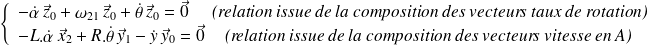
par projection de la relation de composition des vecteurs taux de rotation sur
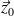 :
:
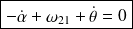
par projection de la relation de composition des vecteurs vitesse :
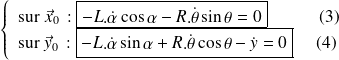
On peut constater qu'il s'agit des deux équations scalaires obtenues par dérivation des équations de la fermeture géométrique (équations
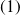 et
et
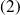 du paragraphe
du paragraphe
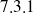 ).
).
Remarque :
Les équations obtenues par fermeture cinématique correspondent aux dérivées des équations obtenues par fermeture géométrique. Les deux approches amènent au même résultat mais la dérivation de la fermeture géométrique conduit généralement au résultat de façon plus efficace.